【IT】AtCoderで腕試し2 - Digits Paradeで詰む

お疲れ様です。
ぜんぜん誇れるスコアじゃないけど記念にヘッダーにして行く立ち回りをするしらせです。

AtCoder2回目の投稿です。

昨日実施された「AtCoder Beginner Contest 135」
今回は、21時ぴったりから制限時間いっぱいの22時40分までしっかり挑戦しました。

もくじ

結果

結果から先に言うと、A,B,Cの3問しか正解できませんでした。
EとかFとかは難しいのかなぁと高を括っていたらDでコケました。。。
　

悔しくて解説資料を見たり解説動画を見たんですが、
いまいち理解できずに深夜までトレースを続けてました。

同じようにここで苦戦している人が多い印象だったので備忘録を作っておきます。

D - Digits Paradeの概要

問題D - Digits Paradeは、数字（0から9）と?で構成された文字列Sが与えられるところから始まります。
文字列Sの?を数字に置き換えてできる整数が13で割った余りが5になるパターンが何通りあるかを調べる問題です。

例えば文字列「?44」の場合。
?を0から9で置き換えたとき、13で割った余りが5になるパターンを調べます
[整数]　→　[あまり]
044　→　5
144　→　1
244　→　10
344　→　6
444　→　2
544　→　11
644　→　7
744　→　3
844　→　12
944　→　8

?44の場合、一番最初の044（先頭が0でも整数として44）だけがパターンに一致します。
また、?1?のように?が2つ以上存在している場合もで同様で、?が2つの場合は少なくとも100通りが考えられます。

問題Cが終わった時点で21時43分だったので、残り1時間もあればなんか行けそうな問題ですよね？

詰まったところ

入力例の上位にあった「??2??5」とか「?44」とかなら力技でループを組んで行けると思うんです。
が、入力例4が問題でした。

＜入力例４＞
?6?42???8??2??06243????9??3???7258??5??7???????774????4?1??17???9?5?70???76???

＜出力例４＞
153716888

（　Д）　　　'゜'゜

?が何個あんねーんｗ
これを実行時間2秒以内に1GBのメモリ空間で実行せよとか無理でしょ。

?の個数分の配列を作って0から9を文字列にそれぞれ当てはめて数値で計算しようか。。。
いやいや、longやInt64でも到底足らん。。。
100000ループするだけでも10秒くらいかかるんだぞ。。。。

うーん。。。

終
制作・著作
━━━━━
ⓃⒽⓀ

ポイント（理解できたところ）

正直、解説のPDF見てもよくわからなかったんですよね。。。
https://img.atcoder.jp/abc135/editorial.pdf
解説さんのようつべライブみて動きは理解しました。
https://youtu.be/brfeRxmzuKw?t=1621

ポイントになるのは剰余算の動作なんですよね。

例えば整数の「123」の場合。13で割った余りって「6」なんですよね。
で、この時実は123を以下のように分解しても成り立つんですよね。

＜各桁で剰余算＞
100 mod 13 = 9
20 mod 13 = 7
3 mod 13 = 3
＜各桁のあまりの合計をさらに剰余算＞
(9+7+3) mod 13 = 6

へーすごい。
これを知らないと（気づかないと）まず解けない。

考え方

（まずは、解説さんのコード内容をトレースのためにすべて手元に書き写しました。）※適当ですみません

各変数の確認。

ここでは2つの配列が利用されています。
long[] dp = new long[N];
　あてはまるパターンの個数を格納する配列。N個分13あります。
　初期値として0を13で割った余りは0なのでdp[0]に1を代入しておきます。
long[] nextDP = new long[N];
　途中計算で使う配列。次の桁の計算が終わるとdpに上書きするために使います。

加えて、超重要な変数が1つあります。
long mul = 1;
　これは、画像の青色で囲まれたブロックで使う変数です。
　この変数は1桁ずつ処理すると以下のような動きをします。
　　1桁目…1
　　2桁目…10
　　3桁目…9
　　4桁目…12
　　・・・
　毎回ループの中で、10を乗算して13で割った余りを格納しています。

　後述のオレンジ色ブロックと緑色ブロックでも説明しますが、各桁の計算では以下のような処理をします。
　　nextDP[(k * mul + j)%N] = dp[j];
　このmulの役割としては、各桁の数値を表すkに対して、予めmod13された各桁目を乗算することで大きな桁数の計算を可能にしているんですね。
　単純に毎回mul *=10;だけをしてしまうと、処理が進むといずれlongの範囲（19桁？）を超えてしまいますからね。
　すごい。（小）

オレンジで囲まれたブロック。
ここでは、文字列のお尻から1文字を抜き出した文字が?の場合に実行するブロックです。

for(int k ...) の箇所
　?を0から9までの数字に当てはめてループ
for(int j ...) の箇所
　わかりにくいので画像にしました。
　これは「5?3」という文字列を実行しているときの2桁目の「?3」の実行中の様子です。
　?(k)が0から9までの10通りの中で13で割った余りが0から12までのいずれかにあてはまるパターンが何個あるかを調べるブロックになっています。
　1つ前の桁で計算したdpの中身を参照するようなロジックですね。
　

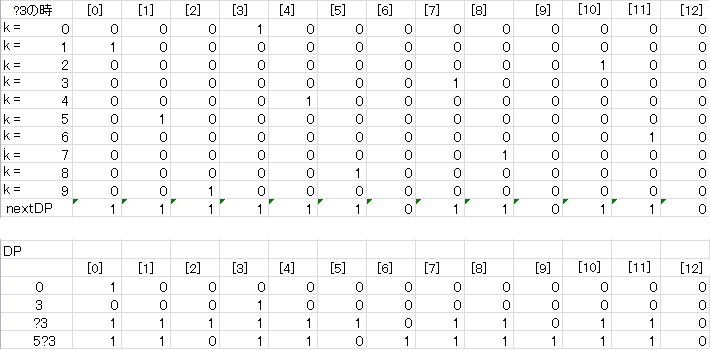
緑色で囲まれたブロック。
ここでは、配列dpの並びを「（各桁の数値を表すk * 桁目mul）mod13」分だけ次の要素に回転するというだけの処理です。
（オレンジのブロックで紹介した画像でいうところの一番最後の2行がそれです。右の要素に6つ回転しています。）
こうやって右シフトをするだけで計算できてしまうのか。。。

答えとしては、最後に配列dp[5]に入っている個数が答えになるわけですね。

はー。。
これで答えがでるんやな。。。

以上
おつでした。